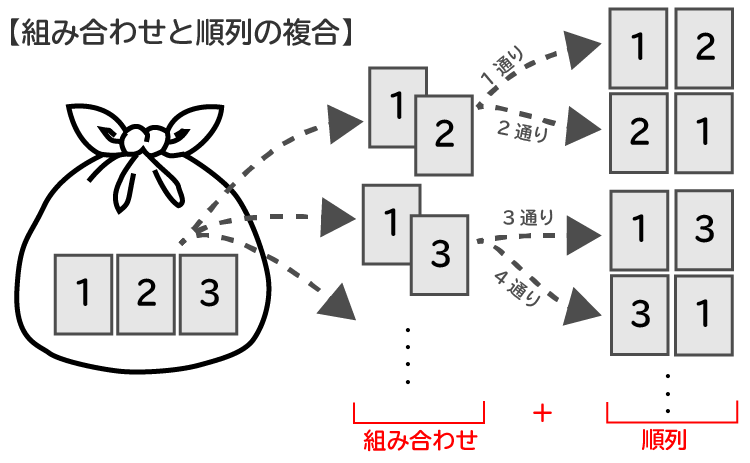
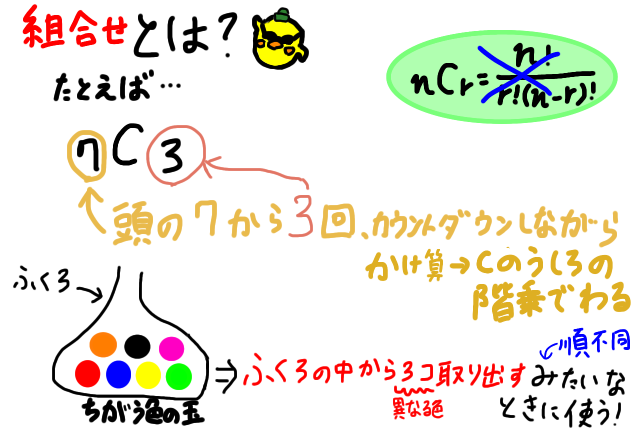
※ C は「組合せ "Combination"」の頭文字 たとえば 3 つの要素から 2 つを取り出す組み合わせなら、以下のように計算でき
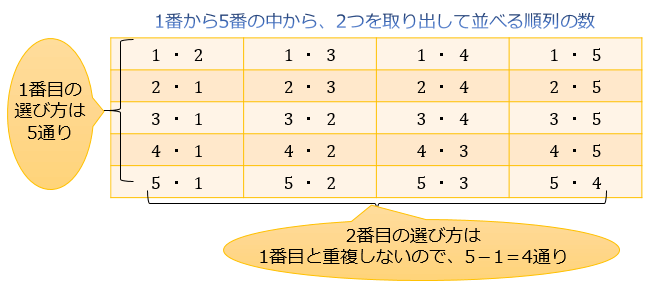
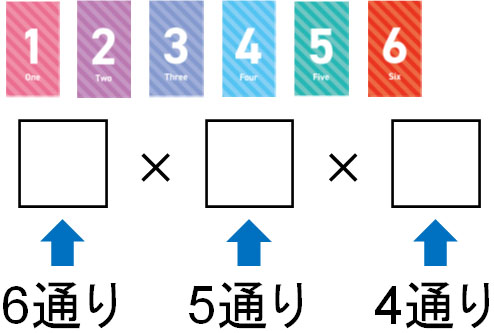
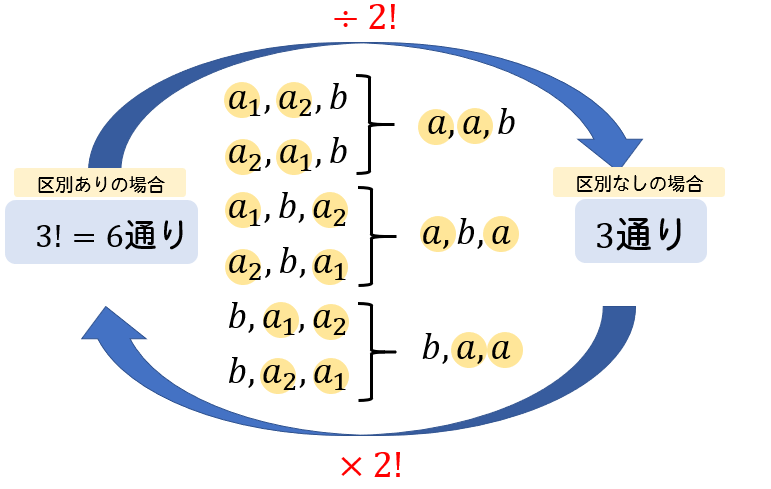
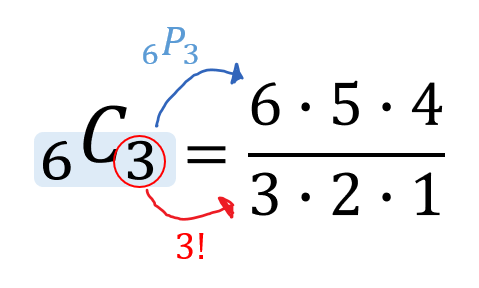
Spi 順列 組み合わせ 公式-Web最初の項が決まれば、選んだ以外の残りの元から第二項を選ぶことができるから、第二項の選び方は (n − 1) 通り、従って 2 順列の総数は n × (n − 1) になる。 同様に、この列の後続項でWeb 組み合わせの公式 n C r = n P r r!
Spi 順列 組み合わせ 公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  | |
 |  | |
「Spi 順列 組み合わせ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 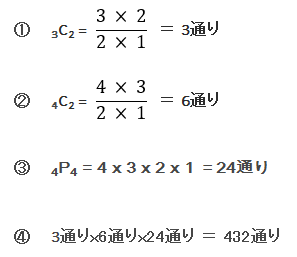 |
 |  |  |
 |  |  |
 |  |  |
「Spi 順列 組み合わせ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  | 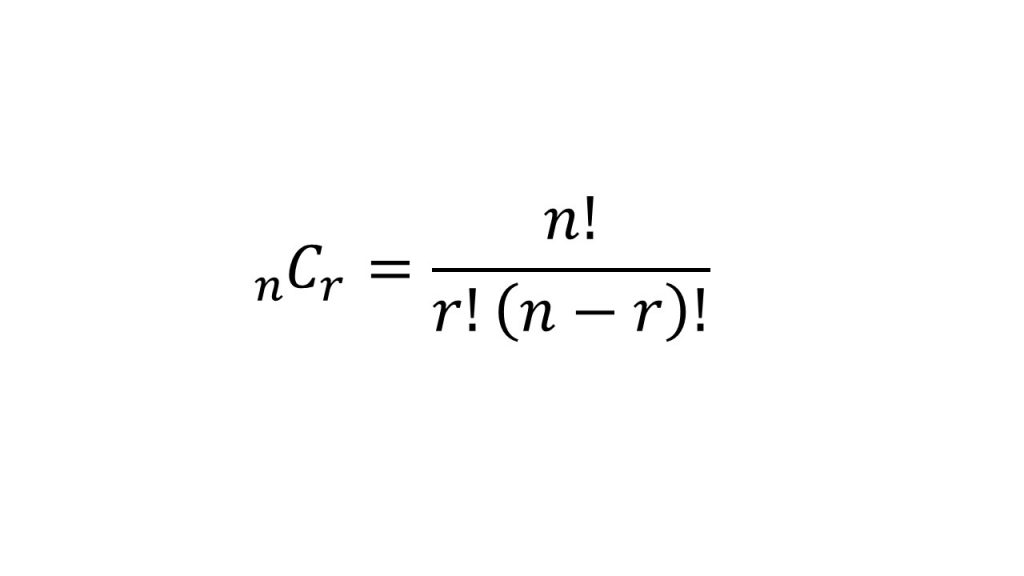 |
「Spi 順列 組み合わせ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  | |
「Spi 順列 組み合わせ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  | |
「Spi 順列 組み合わせ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
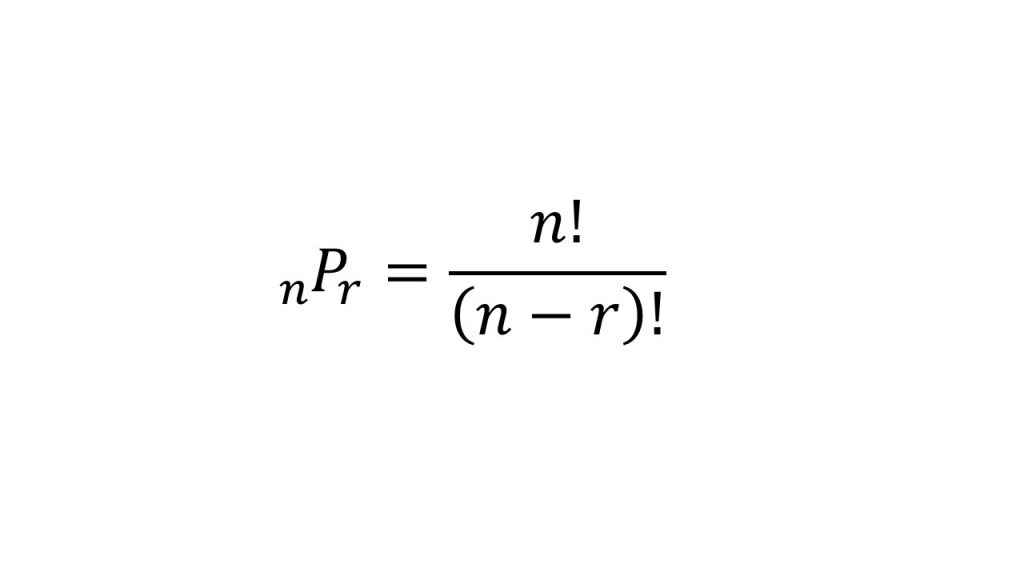 |  |  |
「Spi 順列 組み合わせ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  | |
「Spi 順列 組み合わせ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 | ||
「Spi 順列 組み合わせ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |
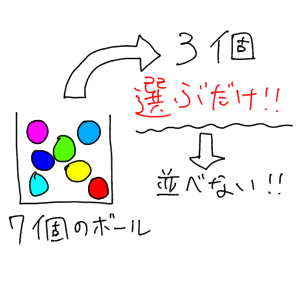
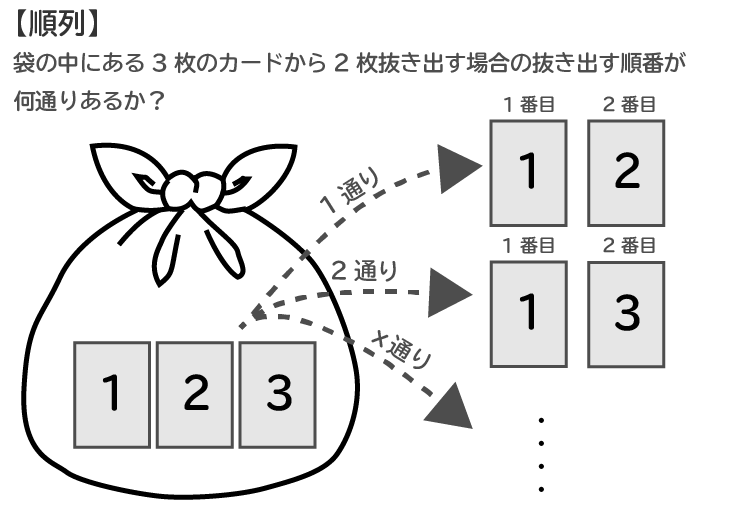
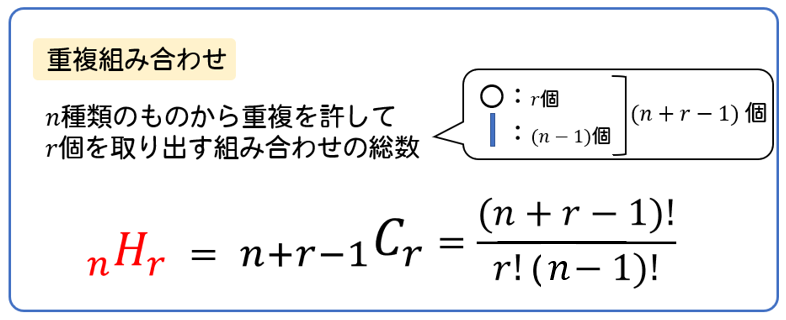
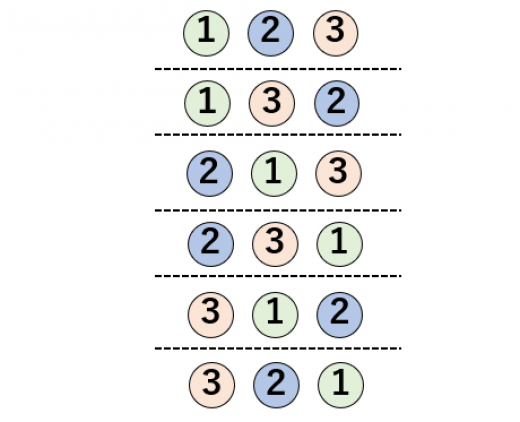
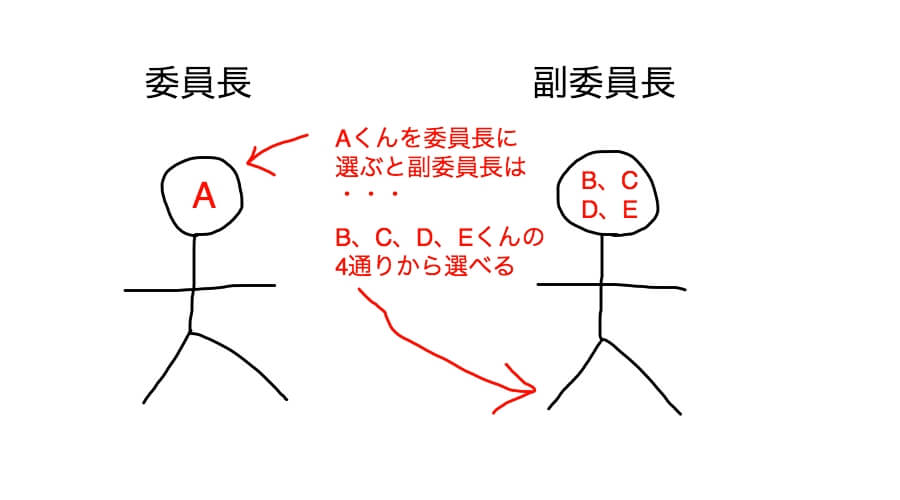
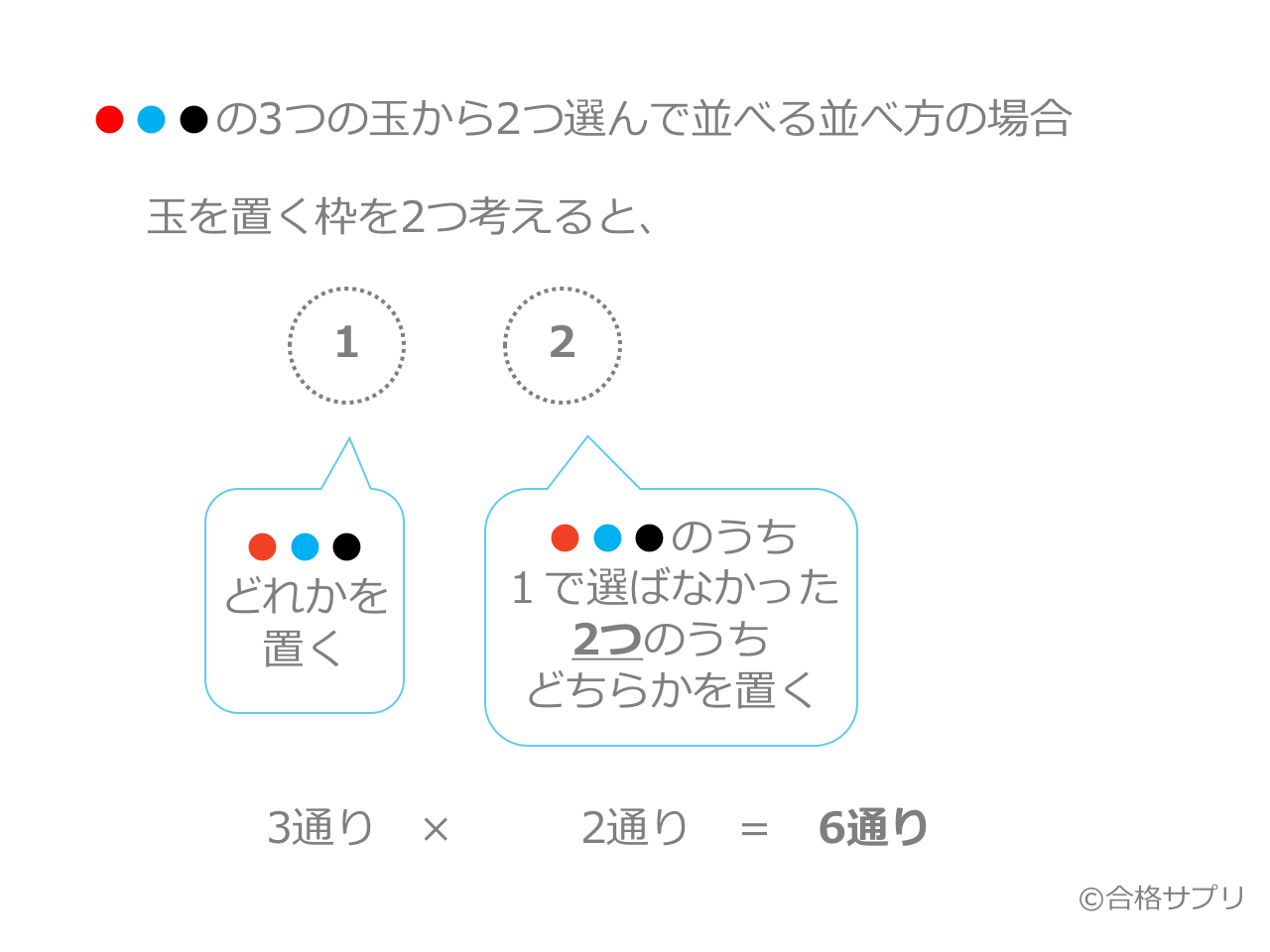
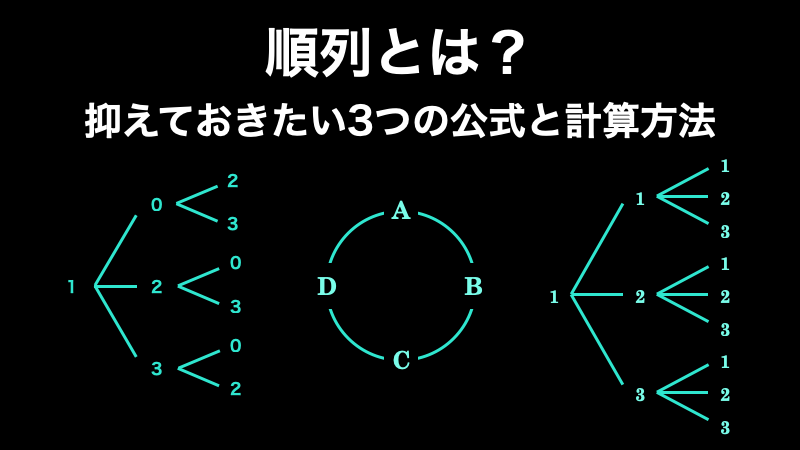
Web順列 (Permutation)とは 順列とは異なるn個の中から異なるr個を取り出して並べる場合の数のことです。 例として、A、B、Cの3つの中から2つを並べる場合を考えましょう。 書き出してWeb組合せ数学 (くみあわせすうがく、 英語 combinatorics )あるいは 組合せ論 (くみあわせろん)とは、特定の 条件 を満たす(普通は有限の)対象からなる集まりを 研究 する 数学 の 分
Incoming Term: 順列 組み合わせ 公式, spi 順列 組み合わせ 公式,




0 件のコメント:
コメントを投稿